概要
大前提 :
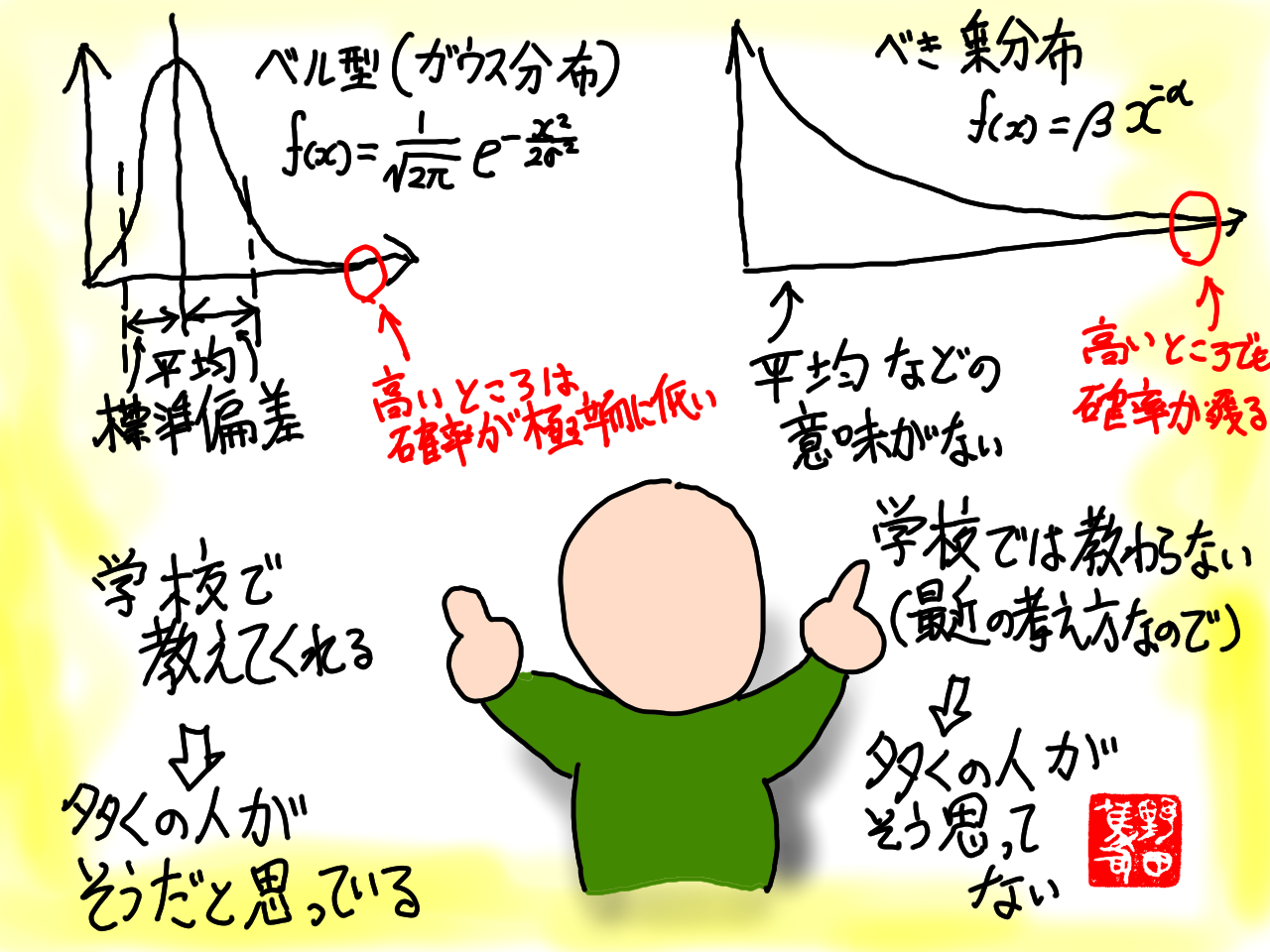
- 基礎研究や斬新な技術開発が生み出す価値の確率分布は、ガウス分布ではなく、べき乗分布
- 斬新な価値を生み出す研究を予測することは不可能
内容
基礎研究や斬新な技術開発・野心的研究に、『選択と集中』を戦略とするのは間違っている。 『選択と集中』とは、研究を始める段階で、「将来的に役に立つ」と思われる研究を選び出して、それに資金を集中するのだが、そもそも「将来的に役に立つ」と判る時点で「斬新」でも「野心的」でもない。 結果、そうやって選ばれた研究の成果は、少しは役に立つかもしれないが、ほとんど斬新でも野心的でもない、凡庸なものしか得られないことになる。
『選択と集中』に対する愚痴は幾ら書いても切りがないほどあるが、この文書の本題ではないし、他の人も多くコメントしているので、これ以上は避ける。
愚痴ばかりでは後ろ向きなので、どうすれば改善できるかを考えた。 『選択と集中』が駄目なら、その逆に、『選択』の反対に『無作為もしくは誰にでも』、『集中』の反対に『細かくばら撒く』と考えたわけだが、いかにも根拠が薄く、乱暴な話である。
そんな時に、書籍「ブラックスワン」
ナシーム・ニコラス・タレブ著 上巻:ISBN-10: 4478001251 ISBN-13: 978-4478001257 下巻:ISBN-10: 4478008884 ISBN-13: 978-4478008881
を読んだ。 その本に影響を受けて、『基礎研究や斬新な技術開発が生み出す価値の確率分布』は、ベル型(ガウス分布)的な確率分布ではなく、べき乗型の確率分布をすると思い当たった。
確率論の復習
急に、ベル型(ガウス分布)やら、べき乗型やらの確率分布の話をされても、確率論の事を忘れた人も多いだろう。 ここで、確率論の復習をしよう
まず、一般用語の復習をしよう。
最初は、確率密度関数
確率論において、連続型確率変数がある値をとるという事象の確率密度を記述する関数であるWikipedia 確率密度関数
だ。
確率密度関数は小文字の f で示される。 なお、引数の x は、ここでは、『基礎研究や斬新な技術開発が生み出す価値』である。
2つ目は、累積分布関数
確率論において、実数値確率変数 X が x 以下になる確率の関数のことWikipedia 累積分布関数
だ。
累積分布関数は大文字の F で示される。 この引数の X は、先の x の範囲が、「-∞から X の間」と言う意味で使われる。
3つ目は、期待値
確率変数のすべての値に確率の重みをつけた加重平均Wikipedia 期待値
だ。
期待値は、上の式のように表される。
また、期待値の一部を切り取ったものは、下の式のように表される。
次のように G を累積分布関数の逆関数とする。 なお、p は確率で、0から1までの値である
当然のことながら、次の式のようになる
最後に、シミュレーションプログラムを作る時のテクニック。 random を0から1までの値を出す一様乱数とすると、f(x)の確率密度分布を持つ x は、次のような乱数で得られる
ガウス分布(ベル型)の場合
ガウス分布(ベル型)の確率密度関数は、次の式のようになる。
なお、ガウス分布の場合、上の式は、引数の x は、平均値からの偏差である。
を『基礎研究や斬新な技術開発が生み出す価値』、
を、その平均、
を、その標準偏差とすると、次のような式で示される。
ガウス確率密度関数の場合、下式のような累積分布関数の一般解は存在しない。
ただし、-∞から+∞の積分は、ガウス積分の公式で1になる
累積分布関数の一般解は存在しないため、その逆関数も存在せず、一様分布乱数からガウス分布を求める時も近似計算などをせざるをえない
また、同様に累積分布関数の一般解は存在しないため、例えば「±3σ内に○○%が入る」と言った計算も近似計算か数値積分せざるを得ない
このため、「±9σの外には○○%が入る」と言った極端な分布は計算しずらく、誤差が大きい。参考 : 正規分布(ガウス分布)の累積分布 数値計算
平均値と標準偏差は、サンプル数が n の時、次の式のように求められる事が知られている。
注意してもらいたいのは、上の式は、あくまで「n個のサンプルでの平均値と標準偏差」であることだ。 有限な個数のサンプルで平均と標準偏差には誤差が含まれる。
ガウス分布の場合、サンプル数が多くなると、平均と標準偏差の誤差が減っていき『真の平均』『真の標準偏差』に近付いていく。
ガウス分布の場合、期待値は、平均値と一致する。
期待値の一部を切り取ったものの一般解は存在しないが、ガウス分布の場合、3σより外の存在確率は急速に減少するために、あまり大きく変化はせず、Xを広い範囲にしても『真の平均値』に近付いて行くだけと考えられる。
べき乗分布の場合
べき乗分布は、一般にはあまり知られていない。確率密度関数は、次の式のように『べき乗分布』するように定義する。
べき乗分布の場合、 x を『基礎研究や斬新な技術開発が生み出す価値』÷『研究や技術開発に必要な資金』とする。 例えば、『100万円の研究資金で、その成果として1000万円の価値を生み出した』の場合なら、『x=10』である。
もし、xが1より、小さい場合は、研究資金より少ない価値しか生み出さなかったわけなので、『損』していることになる。
べき乗分布の場合、確率密度関数の式から、x がマイナスの値を取り扱えない事が判る。
累積分布関数は、次の式のようになる。
の場合
の場合
ただし、累積分布関数は確率であるから、
であり、
かつ、
と言う制約を設け
このような制約を設ける必要がある事自体が「べき乗分布」の課題であることは重々承知している。
、改めて、次の式の様に示すことができる。
べき分布の場合、期待値の一部を切り取ったものの一般解は、次の式のようになる。
の場合
の場合
期待値は、
の場合
の場合
となり、
の場合、期待値は無限大に発散する。
べき乗分布の場合、ガウス分布と異なり、『真の平均』や『真の標準偏差』は存在せず、サンプル数が増え、それに伴い x の範囲も増えると平均も期待値も増大し、特に
の時は無限大に発散する。
G は、累積分布関数の逆関数なので、次の式のようになる。
いよいよ『基礎研究や斬新な研究』の価値創造に『べき乗分布』を当てはめる
一般的なベル型(ガウス分布)に当てはめた場合
100万円の資金(元手)研究が、生み出す価値の平均が80万円で、標準偏差が20万・・とか考えるのがベル型である。
べき乗分布に当てはめた場合
書籍:「ブラックスワン」では、そもそもベル型確率分布を否定して、次のようなべき乗分布を考えるべきだとしている
「100万円の元手なら、10人のうち9人は100万未満だが、1人は100万以上だろう。100人なら、90人は100万以下、9人は1000万以下だが、1人は1000万以上の価値を生む」
言うまでもなく、私の思い付きレベルの『仮説』だ
この計算で行くと、「1億人に1人は、100万円の元手で10兆円の価値を生む」となる
まあ、ジョブズ
ジョブズの逸話では、ガレージにあった中古のトラックを売った金を元手にアップル社を創業したらしい。中古トラックの売値が100万円くらいでアップル社の価値が10兆円くらいだとすると、この計算が成り立つ
とかAmazonのCEO見てると、そのくらいの確率はあり得るかもしれない。
逆にベル型(ガウス分布)だと、ジョブズのような事例は、確率的にありえないほど低い数値
おそらく、30σを超えると思うが、これは、10の100乗分の1より、小さい確率、1兆年の1兆倍の間に1兆分の1も起きない確率である。参照:正規分布(ガウス分布)の累積分布 数値計算
になる。
もちろん、「ブラックスワン」的べき乗確率分布が正しければの話ではあるが・・・
べき乗分布の場合 その1
「100万円の元手なら、10人のうち9人は100万未満だが、1人は100万以上だろう。100人なら、90人は100万以下、9人は1000万以下だが、1人は1000万以上の価値を生む」で考えてみよう。
この場合、累積分布関数から求まる。なお、下式のxは、儲けた金額の元手からの比率である
上の式で、xは0.1以上になることに注意
確率密度関数は、累積分布関数の微分なので直ぐに求められる
期待値の一部を切り取ったものは次のようになる
期待値は次のようになるので、無限大に発散する
期待値の一部を切り取ったものから考察すると、Xは次の式を満たすと、期待値は1より大きくなる(元が取れる)
すなわち
Xを 2203 以上にすると、期待値は1以上になる。つまり、『2万2030人に1人』よりも少ない人数を考慮しなければ、元は取れない計算になる。
べき乗分布の場合 その2
もう少し一般化してみる
「元手を1としたなら、L人のうち(L-1)人は1未満だが、1人は1以上。L×M人なら、(L-1)M人は1以下、(L×M-1)人はN以下だが、1人はN以上の価値を生み、L×M×M人なら1人はN×N以上の価値を生む」で考えてみよう。
「その1」は、L = M = N = 10 の特殊事例である
この場合、累積分布関数から求まる。なお、下式のxは、儲けた金額の元手からの比率である
ただし、
である
ただし、
である
上の式で、xは
以上になることに注意
確率密度関数は、累積分布関数の微分なので直ぐに求められる
期待値の一部を切り取ったものは次のようになる なお、MとNは異なる、つまり a は 1 ではないとしている
期待値は次のようになるので、a が 1 以下なら、無限大に発散する
期待値の一部を切り取ったものから考察すると、Xは次の式を満たすと、期待値は1より大きくなる(元が取れる)
すなわち
Xを 上の式 以上にすると、期待値は1以上になる。 つまり、『
人に1人』よりも少ない人数を考慮しなければ、元は取れない計算になる。
べき乗分布の場合 その3
その2 に、少し具体的な数値を入れてみる
いわゆる 2 8 の法則を当てはめてみよう。
「元手を1としたなら、5人のうち1人は1未満だが、1人は1以上。40人なら、32人は1以下、39人は 10以下だが、1人は 10以上の価値を生み、160人なら1人は 100以上の価値を生む」で考えてみよう。
この例では、「確率が8分の1になる度に、10倍の価値を生む」と言う関係だ
L = 5、M = 8、N = 10 である
Xを 上の式 以上にすると、期待値は1以上になる。 つまり、『
人に1人』よりも少ない人数を考慮しなければ、元は取れない計算になる。
べき乗分布の場合 その4
今の時点では、L と M と N の値も、α と β の値も、測定していないから判らない。
L と M と N の値によって、期待値が変化し、「元の取れる人数」が変化するが、その傾向を示したのが、下の表である。
上の表から、αが小さいほど、少ない人数に分配しても元が取れるが、「αが、どんな値でも、結局は、多人数に分配するほど、期待値が上昇する」傾向にあることが判る。
つまり、これが「基礎研究や斬新な技術開発は、たくさんの人に研究資金を分配したほうが良い」と言う根拠である。